A motivação do texto é responder a pergunta: em uma sala com 50 pessoas qual a probabilidade de pelo menos 2 pessoas fazerem aniversário no mesmo dia ? Somos acostumados a resolver problemas da matemática de forma linear, a famosa regra de 3, contudo esse problema não se resolve de forma linear. Vamos primeiro resolver ele usando regra de 3 e depois da forma correta.
Os vestibulandos sabem que para aplicar regra de 3 é preciso de no mínimo 3 informações, nesse caso ainda só temos uma, precisamos saber quantas pessoas é preciso para essa probabilidade chegar a 100%. Na Teoria Combinatória dos Números existe o Princípio da Casa dos Pombos e ao invés de simplesmente enunciá-lo aqui, vou construir a ideia:
Digamos que você tenha 6 pombos e 5 casas para colocar eles, então você colocando de forma aleatória ou não, com certeza no mínimo 2 pombos estarão na mesma casa. Usando essa ideia para o dia do aniversário temos que o máximo de dias que um ano tem é 366, se eu quero ter certeza que pelo menos 2 pessoas façam aniversário no mesmo dia eu preciso de 367 pessoas.
Ótimo, conseguimos as 3 informações. Aplicando na regra de 3 temos:
367 — 100%
50 — x
367x = 5000%
x = 5000%/367
x = 13.62%
De acordo com esses cálculos a chance de pelo menos 2 pessoas fazerem aniversário no mesmo dia em uma sala com 50 pessoas é de 13.62%, mas esse raciocínio está errado, essa probabilidade não aparece na realidade. Então como podemos fazer de forma correta?
Na graduação temos uma piada que qualquer evento tem 50% de chance de acontecer, pois ou ele acontece ou não acontece, claro que na realidade não é assim mas podemos usar essa ideia. Se somarmos a chance de algum evento acontecer com a chance dele não acontecer vamos obter 100% (isso de forma didática, na matemática existem nomes técnicos para essa situação), considere as seguintes definições para facilitar nossa comunicação:
A = chance de pelo menos 2 das 50 pessoas fazem aniversário no mesmo dia;
B = chance de cada uma das 50 pessoas fazerem aniversário em dias distintos.
Logo, A+B = 1 (não coloquei 100% para facilitar os próximos cálculos mas é a mesma coisa)
Quero descobrir o valor de A, vamos isolá-lo
A = 1 – B
Para resolver basta achar o valor de B, ou seja nosso desafio agora é calcular a probabilidade de 50 pessoas fazerem aniversário em dias diferentes. Vamos usar a fórmula do arranjo simples, ela retorna a quantidade de combinações possíveis, para virar porcentagens basta dividir por 365^50 (365 é o espaço amostral para uma pessoa, como são 50 devemos colocar esse número como potência)
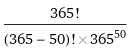
Uma calculadora simples não consegue fazer esses cálculos, então usando o WolfranAlpha (É um software inteligente que roda direto do navegador, linguagens de programação como o python e R provavelmente conseguiriam fazer esses cálculos também) e ele retorna uma aproximação excelente de 0,03 e substituindo esse valor de B na outra expressão temos
A = 1- 0,03
A = 0,97
Ou em porcentagens A = 97%
Portanto, a chance de pelo menos 2 pessoas fazerem aniversário no mesmo dia em uma sala com 50 pessoas é 97%. Além disso conseguimos criar uma função p(n) que retorna a porcentagem a depender do número n de pessoas.
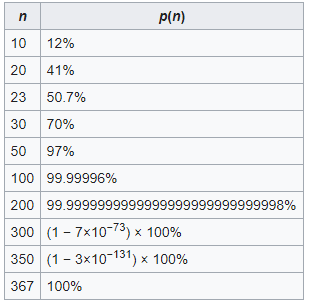
Chequem as referências vou comentar cada uma.
** LIvro
Introdução à Teoria dos Números – José Plinio – O capítulo 3 fala sobre a Teoria Combinatória dos Números muito interessante lá onde eu conheci o princípio da casa dos pombos.
**Links
WolframAlpha Resolve vários problemas incluindo derivadas e integrais.
https://pt.wikipedia.org/wiki/Paradoxo_do_anivers%C3%A1rio – Wikipedia não é uma referência boa para citar em um artigo científico, contudo é um ótimo lugar para se introduzir em um assunto.








